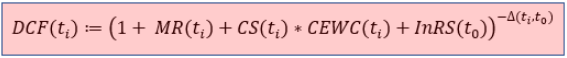The Fair Value DCF is calculated based on the discounted cash flow method. This method takes into consideration all risks associated with financial instruments. These include:
- cash flow timing and variability,
- benchmark market rate risks,
- credit risk (captured through credit spread),
- credit risk mitigation instruments,
- risk of embedded options (captured either through option pricing models or on a retail portfolio level through e.g. prepayment curves),
- liquidity and operational costs (acquired through an initial residual spread incorporated in the discount rate).
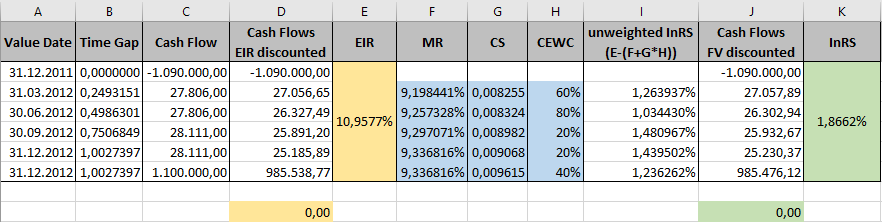
The discounted cash flow method derives the fair value of a loan at time t via
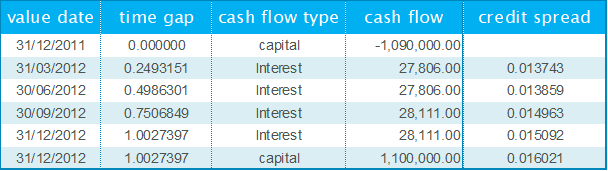
where CF(ti) are the expected future cash flows of the loan. A fair value calculated with the discounted cash flow method differs from the classical present value through the rates used in the discounting: While the classical present value only incorporates the market interest rate, the discount factor DCF(ti) incorporates all of the following elements:
- market interest rate
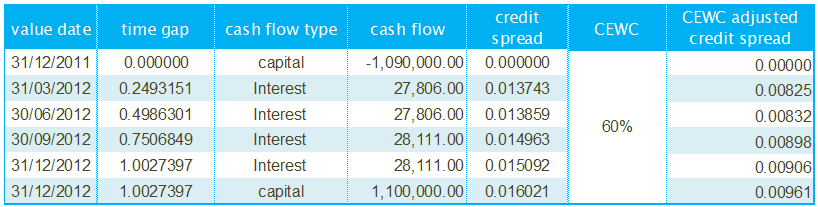
- credit spread and collateral enhancement weighting coefficient
- initial residual spread
To be more precise, the discount factor at payment date ti used in the calculation of fair value is obtained by
where
- MR(ti) denotes the market interest rate at payment date ti,
- CS(ti) stands for the credit spread of the counterparty at payment date ti,
- CEWC(ti) denotes the collateral enhancement weighting coefficient of the deal at payment date ti,
- InRS(t0) stands for the initial residual spread of the deal conclusion date t0 and
- Δ(ti,t0) denotes the time gap between payment date ti and deal conclusion date t0.
Deriving the fair value using the above formula for the discount factor leads to the calculation of a fair value.
Please find below additional information regarding the following topics:
The credit spread is the risk premium on the market interest rate which depends on the credit rating of the counterparty. It represents the yield difference between sound government-issued bonds and corporate bonds.
Example: One deal with customer rating Aaa and one deal with customer rating Ba are considered.The market interest rate is 4% and the funding spread 0.5%. The credit spread for companies with an Aaa rating is 0.25% and the credit spread for companies with a Ba rating is 0.75%. Then the interest rate for the first deal will be 4.75% (= 4% + 0.5% + 0.25%) and the interest rate for the second deal will be 5.25% (= 4% + 0.5% + 0.75%).
Based on the raw statistics delivered, for example probabilities of default, credit spreads can be derived by the solution via various tools and methodologies. Alternatively, credit spreads can be delivered from market data providers, front office or risk system resources.
The following situations may result in a change in credit spreads:
- The change of the personal situation of the counterparty may lead to a change in the rating.
- The change of the micro-economical or macro-economical situation may lead to a change in the credit spread curve assigned to a rating.
Collateral Enhancement Weighting Coefficient
The collateral enhancement weighting coefficient (CEWC) determines a reduction in the credit spread of a loan due to collateral instruments and describes the percentage by which the collateralisation reduces the risk of an asset. It is a constant between 0 and 1. For a loan perfectly covered by collateral, the CEWC will be 0. If a loan has no collateral at all, the CEWC equals 1. In general, if a deal is collateralised with p% of its outstanding payment, its corresponding CEWC is (100-p)%.
In order to determine a CEWC, the following approaches can be used:
- External approach: The entity delivers the credit spread curve which includes the collateral information. In this case, the CEWC will be set to a value of 1.
- Internal approach: The entity delivers the CEWC figure, and the solution takes it into account in the valuation.
- Advanced internal approach: Based on the information delivered for collateral instruments , the solution calculates the CEWC.
For the adjustment of the credit risk related part of the DCF the following steps have to be carried out:
- Determination of the credit spread for each cash flow.
- Valuation of the collateral and calculation of the collateralisation quota (CEWC) related to the outstanding asset.
- Determination of the adjusted credit spreads.
Step 1:
By retrieving the credit spread curve from customer rating and the credit spreads from the time gap, credit spreads for each cash flow are determined:
Step 2:
Colalteral is valued and the corresponding CEWC is computed in relation to the outstanding payment for the deal:
- Outstanding payment: 5 Mio.
- Value of the collateral: 2 Mio.
- CEWC = 1 - (2 Mio. / 5 Mio.) = 60%
Step 3:
Adjusted credit spreads are determined as the product of the original credit spread and the corresponding CEWC:
The initial residual spread (InRS) is a constant value which is calculated as a residual amount on the deal conclusion date. The InRS is calculated so that, on the deal conclusion date, the fair value of the deal on the start date corresponds to the cost of purchase, i.e. on the deal start date, the sum of the discounted cash flows corresponds to the cost of purchase. When the “price” of a financial product (e.g. a loan or a bond) is determined by the bank, several components are taken into account, e.g.
- risk-free market rate
- credit spread
- risk reserve for liquidity risk
- profit centre margin
Due to the following reason, knowing the InRS is important in the accounting world:
- For the representation in the balance sheet and P&L for IFRS, only the market rate and the credit spread are of interest. These portions will be determined by calculating fair value changes.
- Fair value changes are a function of the variables MR, CS and InRS for which the fluctuation of the risk-free interest rates, the credit spreads and the initial residual spread are of relevance.
- Therefore, the rest of the components (e.g. liquidity risk reserve, profit centre margin etc.) will be bundled together and named “Initial Residual Spread”:
Hence, the InRS can be understood as the profit margin of a deal.
Basically, the idea of the InRS is that it will be calculated only once at the beginning of the lifetime of a financial instrument. However, the following situations can be seen as comparable to the “birth” of a new financial instrument so that the InRS has to be recalcualted:
- restructuring of the financial instrument
- buying a long position and selling a short position of a bond
In general, in customer business, the initial residual spread of a deal is determined by the bank and has to be delivered.
If the InRS is not delivered for a deal, it can be calculated by the solution on the basis of the expected cash flows CF(ti) for the deal, the market rates MR(ti) and the corresponding credit spreads CS(ti) and collateral enhancement weighting coefficients CEWC(ti).
To be more precise, in view of the discounted cash flow method, the InRS is calculated so that the mark-to-model fair value of the deal (i.e. the sum of the discounted cashflows) equals its original costs at deal origination date. This is performed by implicitly solving the following non-linear equation with a Newton iteration:
For instance, a concrete situation of calculating an InRS is shown by the following data (columns A, B, C):
Step 1: We calculate the EIR of the deal by performing a goal seek on the sum of the EIR discounted cash flows (Columns D, E).
Step 2: We enter the market interest rates, credit spreads and collateral enhancement weighting coefficients for each cash flow (Columns F, G, H).
Step 3: We calculate an "unweighted InRS" for each cash flow (Column I).
Step 4: We calculate the InRS for the deal by performing a goal seek on the sum of the FV discounted cash flows as described by the above formula (Columns J, K)
As a matter of fact, Steps 1 and 3 are not needed in order to derive the InRs of the deal – they only serve as a comparison between the "unweighted InRSs" per value date with the (global) InRS of the eal.
When the full fair value/hedge fair value is calculated using the discounted cash flow method, so-called forward exchange rates are generally required for deals with cash flows in different currencies. The reason for this logical necessity is to carry out netting [1] of cash flows for deals with cash inflows and outflows and then to discount the netted/balanced cash flows on the valuation date. This is of particular importance since the plus/minus sign of the netted amount is used to decide if the credit spread of the counterparty (for incoming payments) or the bank's credit spread (for outgoing payments) is to be used. It is also relevant if it has been configured in the basic configuration that the in/out rule is to be used for the determination of the market interest rate. (See the chapter "In/Out Rule" in the chapter "Calculation of the Discount Factors".)
Thus these cash flows are first weighted using forward exchange rates and then discounted using the discounted cash flow method.
Taking simple arbitrage considerations into account, forward exchange rates between two currencies can be calculated directly from the spot exchange rates for currencies and the risk-free market interest curves for the individual currencies.
Let us assume that, at the point in time t, the forward exchange rates between the EUR and USD are to be calculated using the spot exchange rate between the EUR and USD and the current yield curves for the two currencies. For the forward exchange rate at the point in time tn, for arbitrage reasons, the following must apply:
Figure: Arbitrage Considerations for Forward Exchange Rates
The forward exchange rate is calculated as follows:
